ルーブリックの詳細 (ID:667)
| タイトル | 数列 ハノイの規則性 |
|---|---|
| 学年 | 高校 |
| 教科 | 算数・数学 |
| 作成者 | Nakatani |
| コメント | 生徒が実際にハノイの塔を使い、数の規則性に気づき、数列の学習意欲が高まるきっかけとなるように指導するとともに、自分の考えをわかりやすく説明したり、証明したりすることを目標とする。今回は、二時間扱う内の一時間目として、次回の数学的帰納法を用いて証明する授業につなげることが目的である。 |
|---|---|
| 画像 | 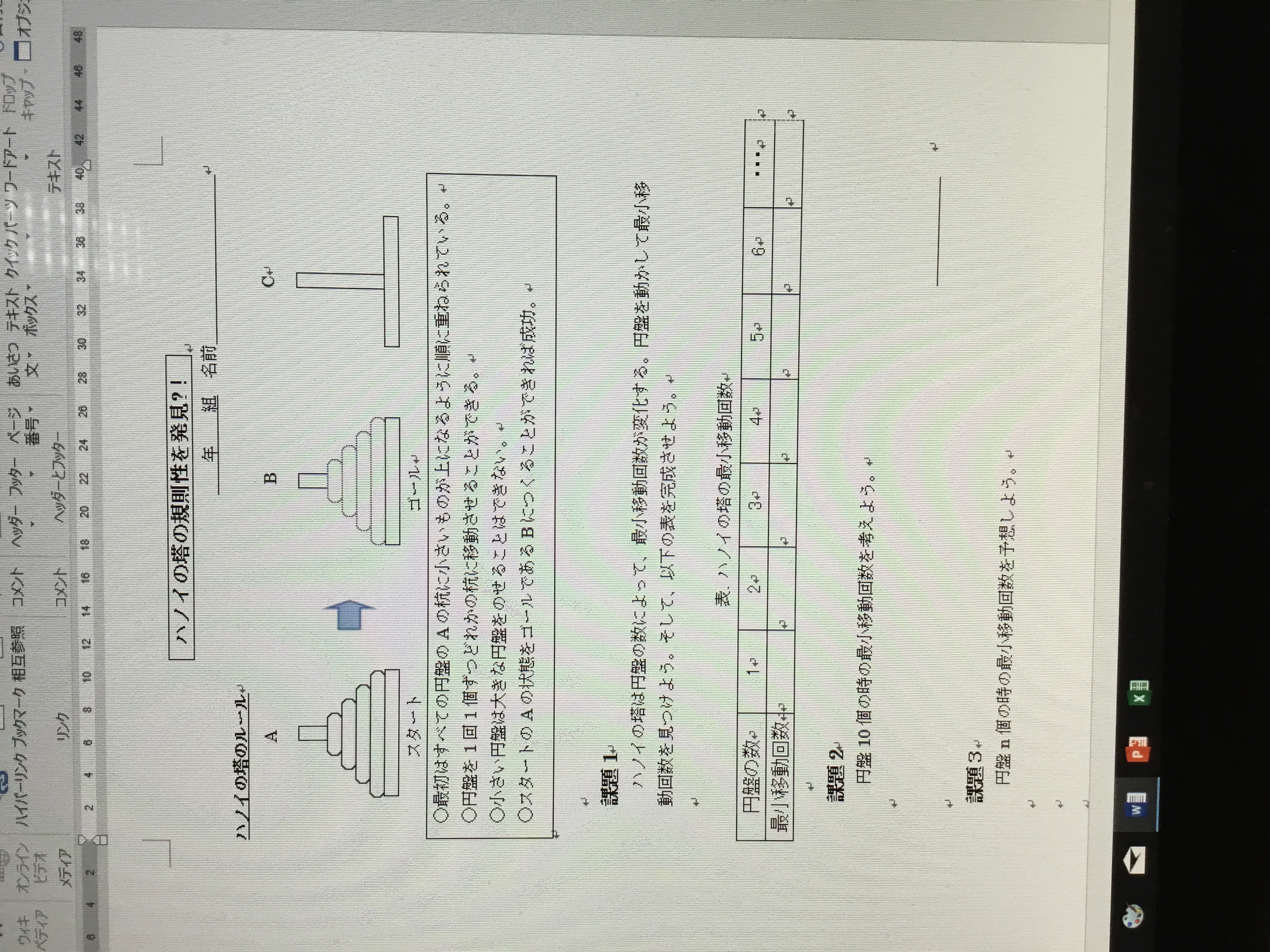 |
収集
- a.課題づくり
- b.図書
- c.ウェブ
- d.アンケート
- e.インタビュー
- f.観察・実験
- g.体験
- h.統計資料
- i.映像
編集(整理・分析)
- j.集約
- k.比較
- l.関連付け
- m.論理
- n.創造
編集(表現)
- o.表・グラフ
- p.レポート
- q.新聞
- r.ポスター・パンフレット
- s.プレゼンテーション
- t.動画
- u.工作・プログラム
- v.劇
発信
- w.発表・イベント
- x.展示・公開
- y.対話
- z.ふりかえり
| 評価規準 | S評価 | A評価 | B評価 | C評価 |
|---|---|---|---|---|
| 思考 最少移動回数の表をつくる | 表を作り上げ、円盤の個数が大きくなったり、n個の時の最小移動回数を考えることができる。 | 表を作り上げ、表を読み解き、最少移動回数の規則性を考えることができる。 | 最少移動回数の表を作り上げることができる。 | ハノイの塔の円盤を動かして、最少移動回数を求めることができる。 |
| 表現 最少移動回数の規則性について説明する。 | 最少移動回数の規則性を予想し、それが正しいのか説明(証明)することができる。 | 最少移動回数の規則性をつかみ、表にはない円盤の数についても予想し、考えをまとめることができる。 | 円盤が増えるごとに、最少移動回数が増えていることをつかみ、規則性について感覚的にまとめている。 | 円盤が増えるごとに、最少移動回数が増えていることをまとめている。 |
参考にしたルーブリック
該当するルーブリックはありません。
派生したルーブリック
該当するルーブリックはありません。